はじめに
キルヒホッフの法則を利用して方程式を立てると、未知数が多くなり、計算が面倒になることがあります。
この記事では、行列を利用して連立方程式を簡単に解く方法を解説していきます。
使い方を覚えれば簡単に解けるようになるので、ぜひ参考にしてください。
例題
今回は以下の例題を使って解説します。
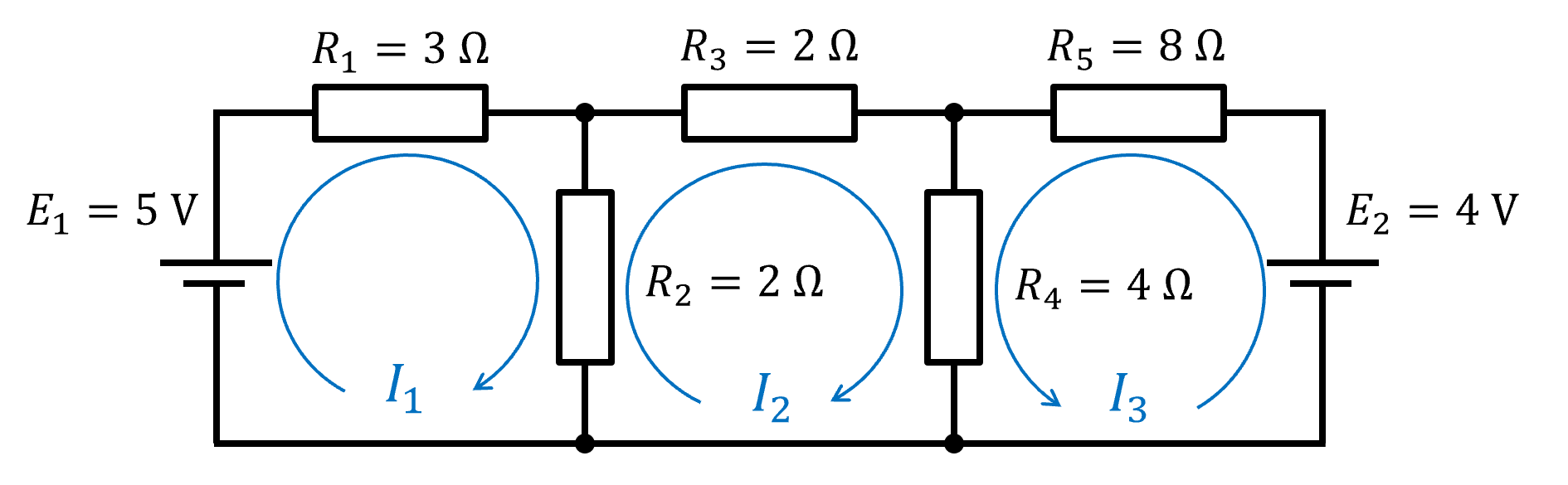
下の回路図でキルヒホッフの法則を用いて、電流 I_1,I_2,I_3 を求めよ。
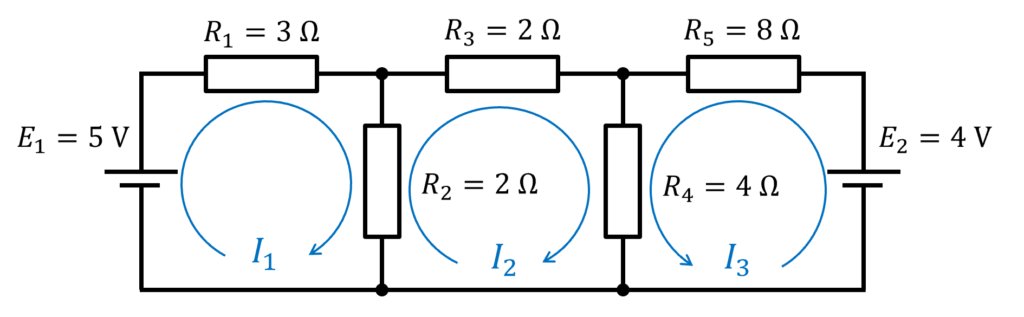
この問題をキルヒホッフの法則を用いて解くと、次の3つの方程式が得られます。
\left\{ \begin{align} (R_1 + R_2)I_1 - R_2 I_2 &= E_1\\ - R_2 I_1 + (R_2 + R_3 + R_4)I_2 + R_4 I_3 &= 0\\ R_4 I_2 + (R_4 + R_5)I_3 &= E_2 \end{align} \right.式が3つになると、加減法や代入法で解くのは現実的ではありませんが、掃き出し法やクラメルの公式を用いることで簡単に解くことができます。
キルヒホッフの法則についての説明は省略しますが、以下の記事で詳しく解説しています。
連立方程式を行列にする
まずは連立方程式を行列で表します。
\begin{pmatrix} R_1+R_2 & -R_2 & 0\\ -R_2 & R_2+R_3+R_4 & R_4\\ 0 & R_4 & R_4+R_5\\ \end{pmatrix} \begin{pmatrix} I_1\\ I_2\\ I_3\\ \end{pmatrix} = \begin{pmatrix} E_1\\ 0\\ E_2\\ \end{pmatrix}左辺の左側の行列は係数行列、左辺の右側の行列は未知数ベクトルを表しています。
例えば、係数行列の1行1列目は、式(1)の I_1 の係数、1行2列目は、式(1)の I_2 の係数、1行3列目は、式(1)の I_3 の係数に対応しています。
抵抗値と電圧が与えられているので、代入します。
\begin{pmatrix} 5 & -2 & 0\\ -2 & 8 & 4\\ 0 & 4 & 12\\ \end{pmatrix} \begin{pmatrix} I_1\\ I_2\\ I_3\\ \end{pmatrix} = \begin{pmatrix} 5\\ 0\\ 4\\ \end{pmatrix}解法1:掃き出し法
掃き出し法とは
上の行列で係数行列の右に定数項を並べた行列を拡大係数行列といい、次のように表します。
\left( \begin{array}{ccc|c} 5 & -2 & 0 & 5\\ -2 & 8 & 4 & 0\\ 0 & 4 & 12 & 4\\ \end{array} \right)掃き出し法では、上の拡大係数行列に、次の3つの操作を行って簡約行列を作ります。
- 行の入れ替え
- 行を定数倍する
- 行どうしを足し引きする
最終的に次のような簡約行列を目指して上の操作を行います。この行列になると、連立方程式が解けたことになります。
\left( \begin{array}{ccc|c} 1 & 0 & 0 & I_1\\ 0 & 1 & 0 & I_2\\ 0 & 0 & 1 & I_3\\ \end{array} \right)掃き出し法を使って解く
それでは、実際に掃き出し法で解いてみます。
\left( \begin{array}{ccc|c} 5 & -2 & 0 & 5\\ -2 & 8 & 4 & 0\\ 0 & 4 & 12 & 4\\ \end{array} \right)↓3行目を4で割る(計算を楽にするため)
\left( \begin{array}{ccc|c} 5 & -2 & 0 & 5\\ -2 & 8 & 4 & 0\\ 0 & 1 & 3 & 1\\ \end{array} \right)↓1行目と2行目を入れ替える(1行1列目を1にしやすくする)
\left( \begin{array}{ccc|c} -2 & 8 & 4 & 0\\ 5 & -2 & 0 & 5\\ 0 & 1 & 3 & 1\\ \end{array} \right)↓1行目を−2で割る(1行1列目を1にする)
\left( \begin{array}{ccc|c} 1 & -4 & -2 & 0\\ 5 & -2 & 0 & 5\\ 0 & 1 & 3 & 1\\ \end{array} \right)↓1行目の−5倍を2行目に足す(2行1列目を0にする)
\left( \begin{array}{ccc|c} 1 & -4 & -2 & 0\\ 0 & 18 & 10 & 5\\ 0 & 1 & 3 & 1\\ \end{array} \right)↓2行目と3行目を入れ替える(2行2列目を1にする)
\left( \begin{array}{ccc|c} 1 & -4 & -2 & 0\\ 0 & 1 & 3 & 1\\ 0 & 18 & 10 & 5\\ \end{array} \right)↓2行目の4倍を1行目に足し、−18倍を3行目に足す
(2列目の上下の成分を0にする)
↓3行目を−44で割る(3行目の先頭を1にする)
\left( \begin{array}{ccc|c} 1 & 0 & 10 & 4\\ 0 & 1 & 3 & 1\\ 0 & 0 & 1 & 13/44\\ \end{array} \right)↓3行目の−10倍を1行目に足し、−3倍を2行目に足す
(3列目の上にある成分を0にする)
このように斜めに1が並び、それ以外が0になると、連立方程式が解けたことになります。
拡大係数行列の右側の部分が I_1, I_2, I_3 の値になり、
I_1 = \frac{23}{22} \mathrm{\,[A]}, \, I_2 = \frac{5}{44} \mathrm{\,[A]}, \, I_3 = \frac{13}{44} \mathrm{\,[A]}と求まりました。
掃き出し法の特徴
実は掃き出し法は、加減法で連立方程式を解く場合と、ほとんど同じ操作をしています。
機械的に解くことができるので、未知数が増えても対応しやすく、基本的に最も速く解くことができます。
抵抗値や電圧が未知数の場合は、クラメルの公式を使った方が速くなることがありますが、抵抗値や電圧が数値の場合は掃き出し法がおすすめです。
解法2:クラメルの公式
クラメルの公式は、行列式を使って連立方程式を解く方法です。
まずは、係数行列の行列式 |A| を求めます。
行列が3×3なので、サラスの公式を用いると、
\begin{aligned} |A| &= \begin{vmatrix} 5 & -2 & 0\\ -2 & 8 & 4\\ 0 & 4 & 12\\ \end{vmatrix} \\ &= 5 \cdot 8 \cdot 12 - (-2) \cdot (-2) \cdot 12 - 5 \cdot 4 \cdot 4 \\ &= 352 \end{aligned}と求まります。
次に I_1 を求めます。
I_1 は、 I_1 の係数部分を、右辺の \begin{pmatrix} 5\\ 0\\ 4\\ \end{pmatrix} で置き換えた行列の行列式を |A| で割ることで求まります。
よって、
\begin{aligned} I_1 &= \frac{1}{|A|} \begin{vmatrix} 5 & -2 & 0\\ 0 & 8 & 4\\ 4 & 4 & 12\\ \end{vmatrix} \\ &= \frac{1}{352} \left\{ 5 \cdot 8 \cdot 12 + 4 \cdot 4 \cdot (-2) - 5 \cdot 4 \cdot 4 \right\} \\ &= \frac{368}{352} = \frac{23}{22} \end{aligned}となり、同様に I_2, I_3 を計算すると、
\begin{aligned} I_2 &= \frac{1}{|A|} \begin{vmatrix} 5 & 5 & 0\\ -2 & 0 & 4\\ 0 & 4 & 12\\ \end{vmatrix} \\ &= \frac{1}{352} \left\{ -5 \cdot (-2) \cdot 12 - 5 \cdot 4 \cdot 4 \right\} \\ &= \frac{40}{352} = \frac{5}{44} \end{aligned} \begin{aligned} I_3 &= \frac{1}{|A|} \begin{vmatrix} 5 & -2 & 5\\ -2 & 8 & 0\\ 0 & 4 & 4\\ \end{vmatrix} \\ &= \frac{1}{352} \left\{ 5 \cdot 8 \cdot 4 + 5 \cdot 4 \cdot (-2) - 4 \cdot (-2) \cdot (-2) \right\} \\ &= \frac{104}{352} = \frac{13}{44} \end{aligned}と求まります。
クラメルの公式の特徴
この問題では、クラメルの公式の方が、掃き出し法よりも計算量が多くなります。
クラメルの公式では、各未知数ごとに行列式を計算する必要があるため計算量が多くなりますが、2行の行列式であれば比較的簡単に計算できます。
そのため、行列が2行の場合や、抵抗値や電圧の値が未知数の場合はクラメルの公式もおすすめです。
まとめ
キルヒホッフの法則で立てた連立方程式は、基本的に掃き出し法を使った方が速く解くことができます。
ただし、行列が2行で抵抗値や電圧の値が未知数の場合は、クラメルの公式の方が速くなる場合があります。
- 抵抗値や電圧が数値 → 掃き出し法
- 3行以上 → 掃き出し法
- 抵抗値や電圧が未知数, 2行 → クラメルの公式
この記事が参考になれば幸いです。ここまで読んでいただきありがとうございました。

コメント