はじめに
この記事では、電気回路の問題を解く上でよく利用されるキルヒホッフの法則について解説していきます。
キルヒホッフの法則を理解することで、複雑な回路でも簡単に電流や電圧を求めることができるようになります。
電気回路が苦手な方でも理解できるように、分かりやすく解説していきます。
キルヒホッフの法則とは
まず、キルヒホッフの法則には、電流則と電圧則があります。
電流則は、「キルヒホッフの第1法則」や「KCL (Kirchhoff’s Current Law)」と表記され、電圧則は、「キルヒホッフの第2法則」や「KVL (Kirchhoff’s Voltage Law)」と表記されることがあります。
電流則 (第1法則)
電流則(第1法則)は、「回路のどの節点においても、出入りする電流の総和が0になる」という法則です。
下図のような節点(回路の接続点)に流れる電流を考えます。
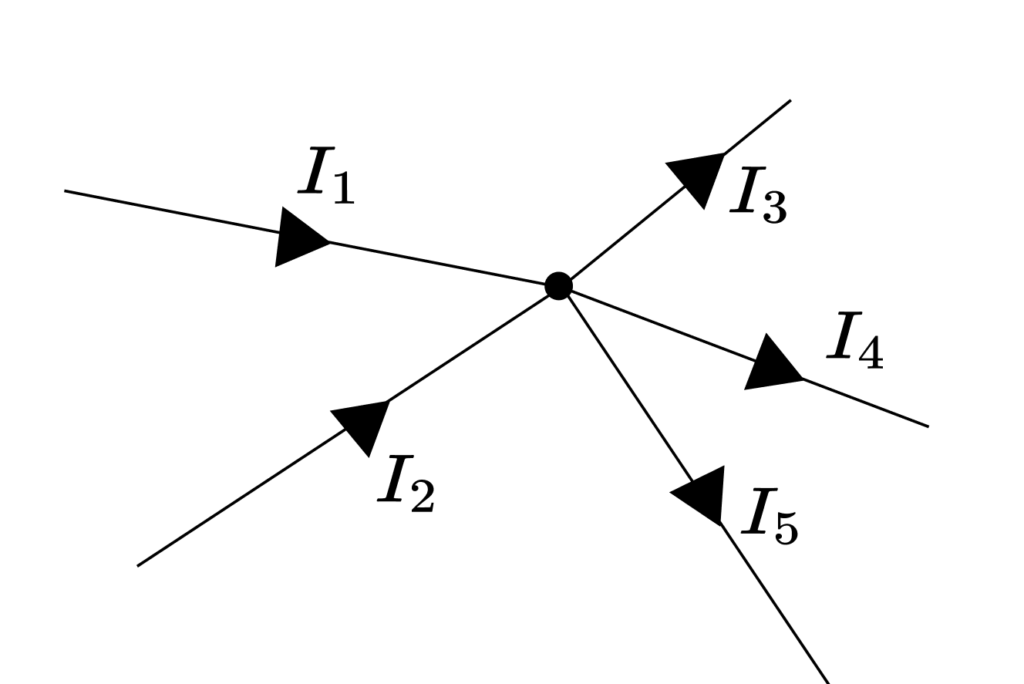
節点では、流れてきた電流がなくなったり、増えたりすることはないので、節点から流出する電流は流入する電流と等しくなります。
「節点に入る電流と節点から出る電流が等しい」ということは、節点から出る電流をマイナスとすることで、「出入りする電流の総和が0になる」と同じ意味になります。
式で表すと次のようになります。
I_1 + I_2 = I_3 + I_4 + I_5(節点に入る電流と節点から出る電流が等しい)
I_1 + I_2 - I_3 - I_4 - I_5 = 0(出入りする電流の総和が0になる)
電圧則 (第2法則)
電圧則(第2法則)は、「回路のどのループにおいても、電圧上昇の和と電圧降下の和は等しい」という法則です。
ループとは、回路をある経路で1周するルートのことを言います。ループは、1つの回路において複数存在する場合が多く、複雑な回路になるほどループの数は多くなります。
例えば、下の回路では、赤、青、緑の3つのループが存在します。
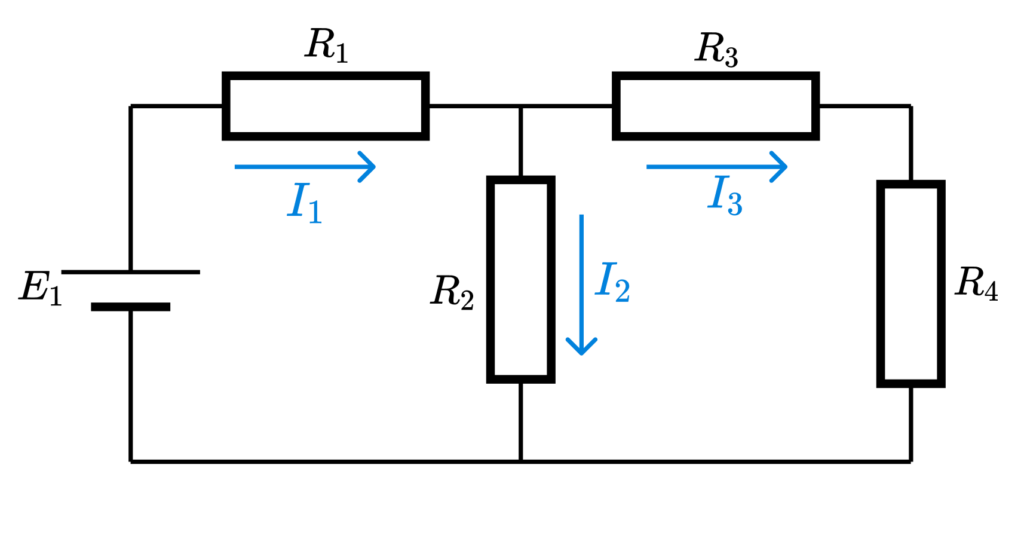
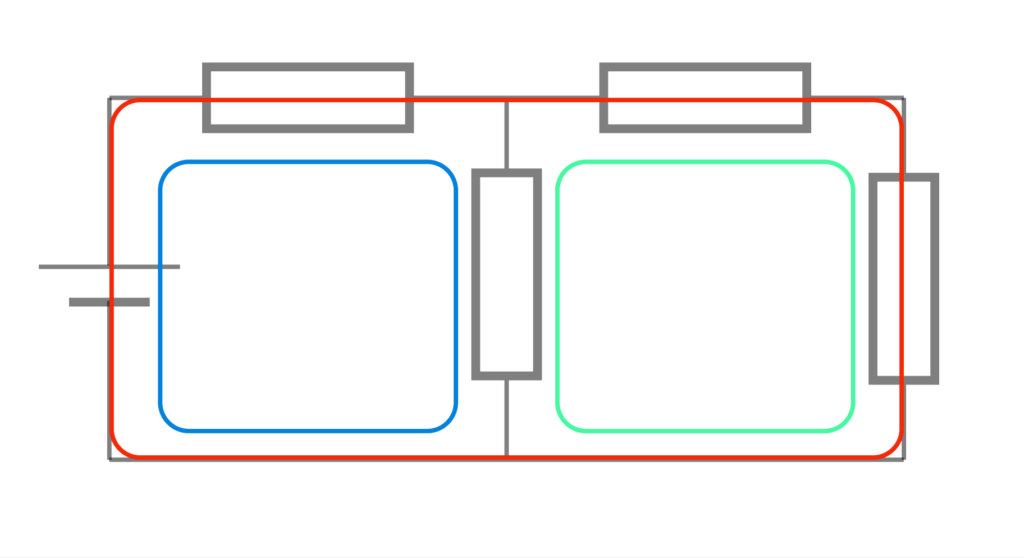
電圧則より、これら3つのループにおいて、電圧上昇の和と電圧降下の和が等しくなります。
赤のループでは、電圧上昇の和が起電力 E_1 、電圧降下の和が3つの抵抗に加わる電圧となり、次式が成り立ちます。
E_1 = R_1 I_1 + R_3 I_3 + R_4 I_3 = R_1 I_1 + (R_3 + R_4) I_3同様に、青のループでは、次式が成り立ちます。
E_1 = R_1 I_1 + R_2 I_2緑のループでは電源はありませんが、電流の流れから抵抗 R_2 の両端の電圧 R_2 I_2 を電圧上昇として扱い、抵抗 R_3 と R_4 の両端の電圧 (R_3 + R_4) I_3 を電圧降下として扱います。
これは、電圧上昇と電圧降下を逆に考えてもOKです。
R_2 I_2 = (R_3 + R_4) I_3キルヒホッフの法則の使い方
問題を解きながら説明した方が分かりやすいと思うので、次の問題を解いてみます。
下図において、抵抗 R_1, R_2 に流れる電流 I_1, I_2 の大きさと向きをそれぞれ求めよ。
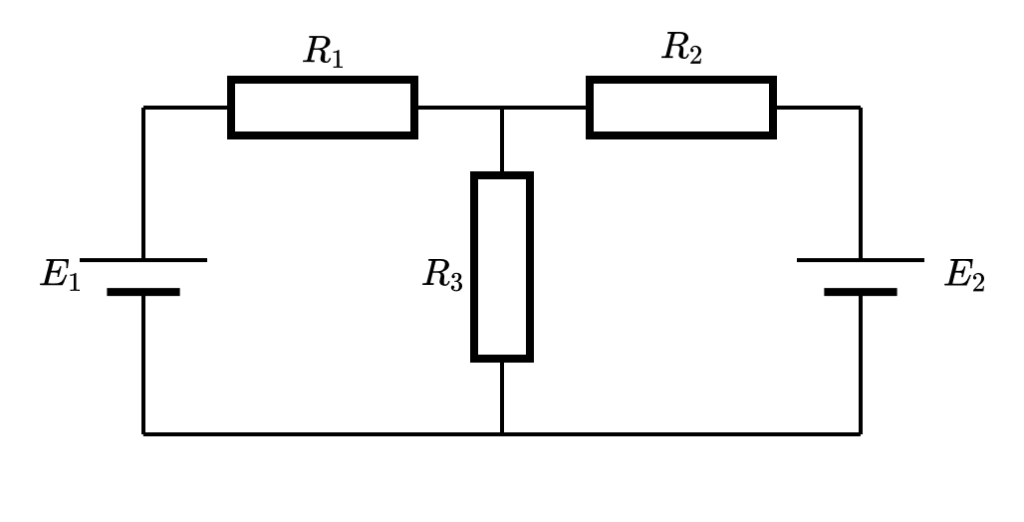
キルヒホッフの法則を利用した解き方には、枝電流法、閉路電流法(ループ電流法)と節点電圧法があります。
今回は簡単にループの電流を求めることができる閉路電流法で解いていきます。
ループを選ぶ
この問題では、3つのループが考えられますが、閉路電流法では内部にループを含まない最小のものを選びます。下図のように、赤のループは内側にループを含むので、青と緑のループを選びます。
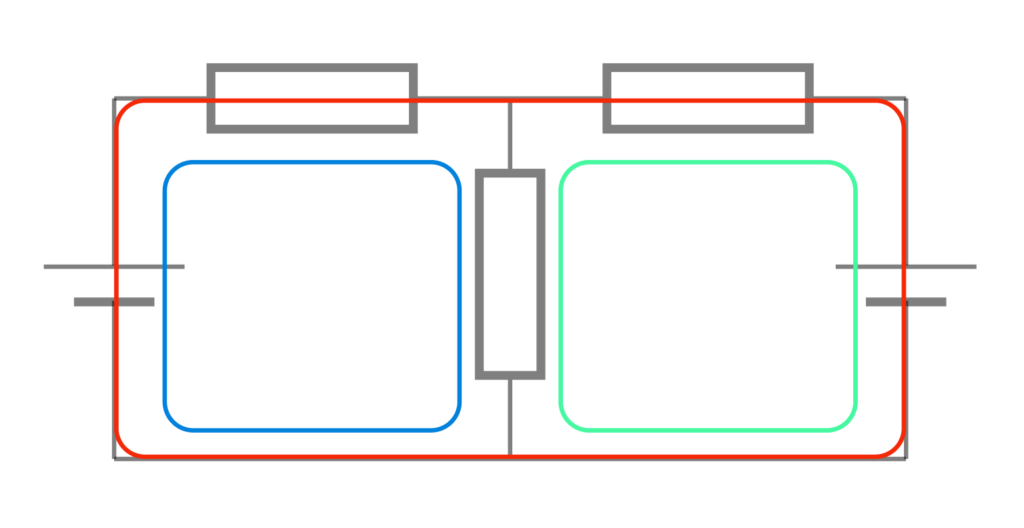
ループ電流を決める
次は、選んだループに電流を割り当てます。
ループ電流の向きは、時計回りでも反時計回りでも大丈夫ですが、問題文で数値が与えられていた場合に、間違った電流の向きを選ぶと電流がマイナスの値になります。
今回は下図のような向きでループ電流 I_1, I_2 を割り当てます。
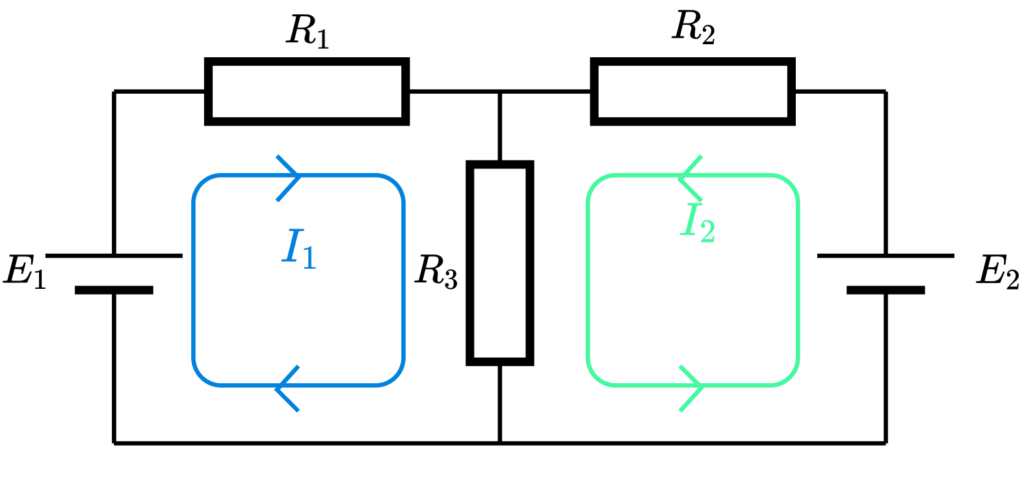
ここまでで方程式を立てる準備ができました。
電圧則を使って方程式を立てる
次は、電圧則(KVL)を使って方程式を立てていきます。
ここで注意する必要があるのは、 R_3 の電流です。 R_3 はどちらのループでも通っているので、電流は I_1 と I_2 を使って表す必要があります。
青のループから見ると、抵抗 R_3 に流れる電流 I_1 と同じ向きに I_2 が流れているので、青のループについての方程式は次のようになります。
E_1 = R_1 I_1 + R_3 (I_1 + I_2)緑のループでも、抵抗 R_3 に流れる電流 I_2 と同じ向きに I_1 が流れているので、緑のループについての方程式は次のようになります。
E_2 = R_2 I_2 + R_3 (I_1 + I_2)今回の場合は、電流の向きと電源の向きが一致していますが、逆になっていた場合は電源電圧にマイナスをつける必要があります。
連立方程式を解く
あとは、これらの方程式を連立して解くだけです。
E_1 = R_1 I_1 + R_3 (I_1 + I_2) E_2 = R_2 I_2 + R_3 (I_1 + I_2)連立方程式を解く過程は省略しますが、答えは以下のようになります。
電流の大きさ:
I_1 = \frac{(R_2 + R_3) E_1 - R_3 E_2}{R_1 R_2 + R_1 R_3 + R_2 R_3} I_2 = \frac{(R_1 + R_3) E_2 - R_3 E_1}{R_1 R_2 + R_1 R_3 + R_2 R_3}電流の向き:

連立方程式の計算については、以下の記事を参考にしてください。
おわりに
この記事では、キルヒホッフの法則について解説しました。
キルヒホッフの法則を理解することで、複雑な回路でも機械的に解くことができるようになるので、様々な問題を解いて理解を深めてみてください。
ここまで読んでいただきありがとうございました。


コメント