はじめに
この記事では、大学生向けに交流回路の力率について解説します。
交流回路の中でも理解が難しいところなので、フェーザ図や例題を使って分かりやすく説明します。
ぜひ最後まで読んでください。
力率とは
交流の電力
力率を理解するには、有効電力・無効電力・皮相電力の関係が重要になります。
それぞれの電力は、次のような意味があります。
| – | 単位 | 説明 |
|---|---|---|
| 有効電力 P | [W](ワット) | 負荷で消費される電力 |
| 無効電力 Q | [var](バール) | 負荷で消費されない電力 電源と負荷の間を行ったり来たりする |
| 皮相電力 S | [VA](ボルトアンペア) | 電源から供給された電力の総量 有効電力と無効電力のベクトル和 |
有効電力は負荷(抵抗)で消費される電力で一般的な電力といえば有効電力を指します。
しかし、コイル(インダクタ)やコンデンサ(キャパシタ)はエネルギーを蓄えるだけで実際に消費されず、電源にエネルギーが戻っていきます。このエネルギーを無効電力といいます。
また、無効電力は負荷で消費されませんが、電源と負荷の間を流れています。
無効電力と有効電力を合わせた電力を皮相電力といい、電源から供給された電力の総量を表します。
この関係を図で表すと次のようになります。
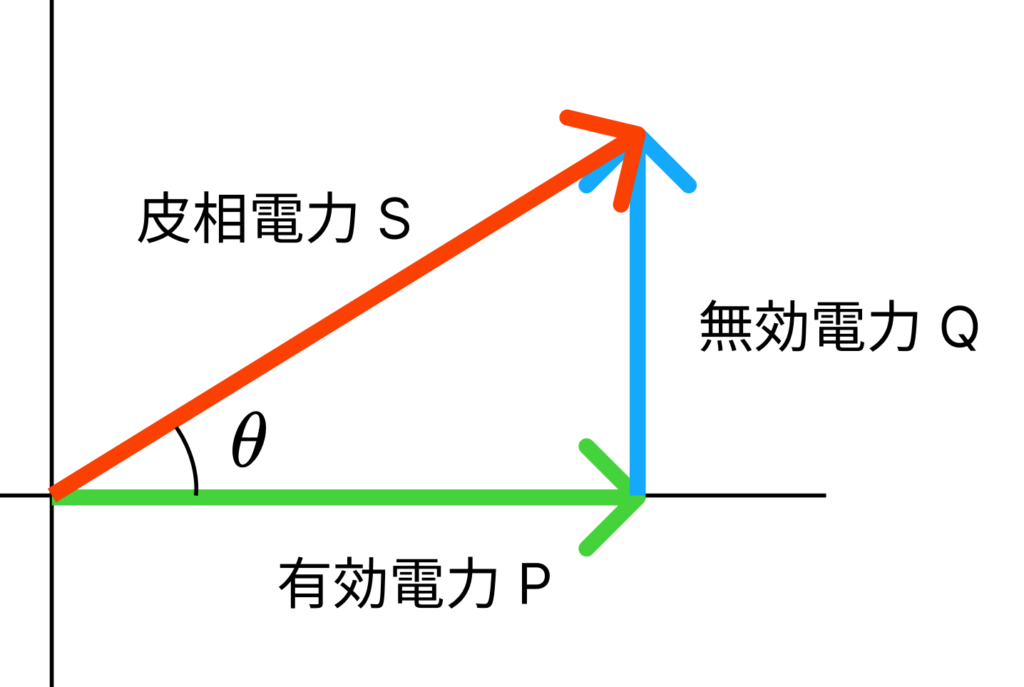
\theta は、電圧と電流の位相差です。
皮相電力は、電圧と電流の実効値を掛けることで求められます。
S = V_{rms} I_{rms}rmsは実効値(Root Mean Square)のことです。
有効電力は、皮相電力に \cos{\theta} を掛けることで求められ、無効電力は \sin{\theta} を掛けることで求められます。
P = S \cos{\theta} = V_{rms} I_{rms} \cos{\theta} Q = S \sin{\theta} = V_{rms} I_{rms} \sin{\theta}力率は有効電力の割合
力率(Power Factor)は、皮相電力に対する有効電力の割合を表します。
そのため、有効電力と皮相電力の関係から、
PF = \frac{P}{S} = \cos{\theta}となり、 \cos{\theta} が力率になります。
力率は有効電力の割合なので、0から1の値になり、一般的にはマイナスにはなりません。
100を掛けて%で表すこともあります。
力率が1の場合
力率が1になるのは電圧と電流の位相差が0になる時です。
例えば、交流電源に抵抗を接続すると電圧と電流は以下のようになります。
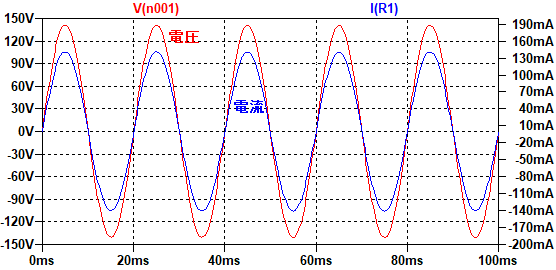
電圧と電流の波形は、時間方向のずれがなく位相差はありません。
この場合、力率は1となり、皮相電力の100%が有効電力として使われることになります。
無効電力が0になるので、最も効率がいい状態です。
力率が0の場合
一方で、コイルやコンデンサを接続すると位相差が発生します。
コイルは、電流が電圧よりも90°遅れる性質があるため、位相差は \frac{\pi}{2} です。
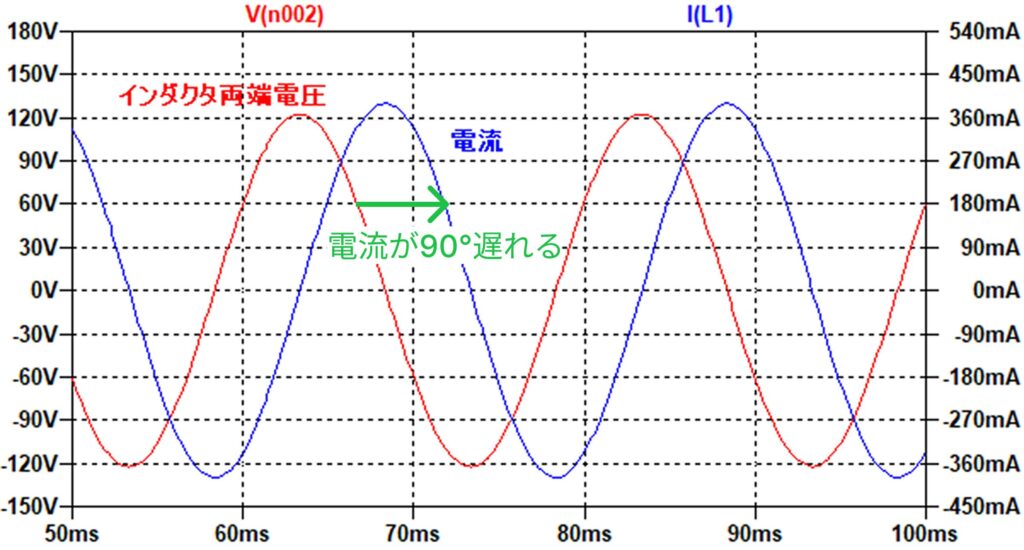
よって力率は、 \cos{ \frac{\pi}{2} } = 0 となり、皮相電力がすべて無効電力として使われています。
コイルでは電力が消費されず、電源とコイルでエネルギーが行ったり来たりしているだけなので、効率が悪いです。
力率の求め方
力率の求め方を例題を用いて解説していきます。
例題1: RL直列回路の力率
抵抗 R= 10\mathrm{\,\Omega} とインダクタンス L = 0.1\mathrm{\,H} を直列に接続した負荷に、周波数 f = 50\mathrm{\,Hz} , 電圧 V = 100\mathrm{\,V} (実効値)の交流電圧を加えた。
この回路の力率を求めよ。
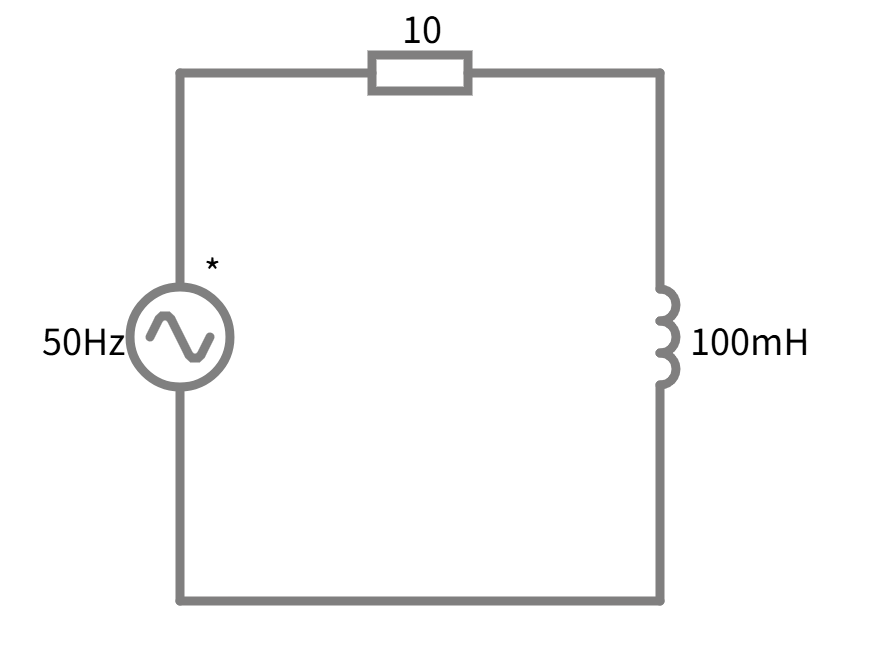
力率は \cos{\theta} で求められるため、電圧と電流の位相差が分かれば求められます。
位相差はインピーダンス角 \theta と等しくなるので、合成インピーダンス \dot{Z} を求めます。
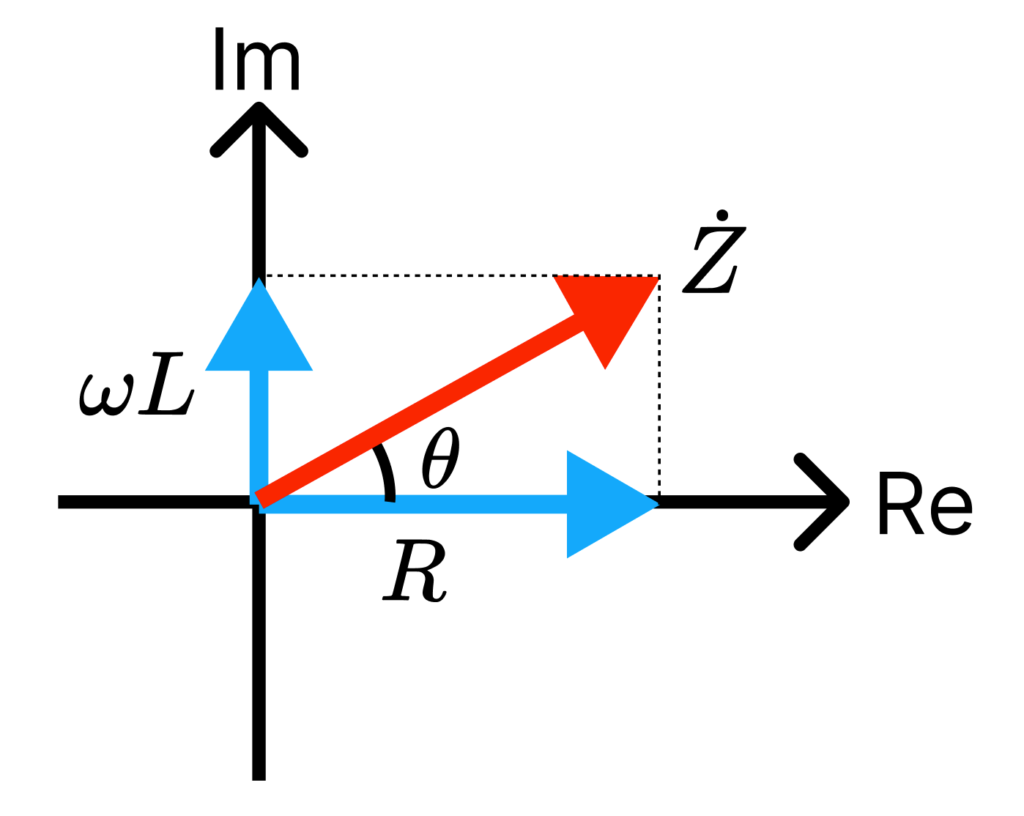
合成インピーダンスは、 \dot{Z} = R + j \omega L となるので、
PF = \cos{\theta} = \frac{R}{|\dot{Z}|} = \frac{R}{\sqrt{R^2 + (\omega L)^2}} = \frac{10}{\sqrt{10^2 + (2 \pi \cdot 50 \cdot 0.1)^2}} \approx 0.30となり、力率は0.30と求まります。
例題2: 誘導電動機の力率改善
ある工場で、三相誘導電動機が有効電力 P = 50\mathrm{\,kW} 、力率 0.7 で稼働している。
力率を 0.95 に改善するために必要な無効電力の補償量(コンデンサによる供給分)を求めよ。
三相誘導電動機はコイルがあるため電流が電圧よりも遅れ、力率が低下します。
一方で、コンデンサは、電流が電圧よりも進む性質があるため、位相差が小さくなり力率を改善することができます。
力率改善前のパワートライアングルは次のようになっています。
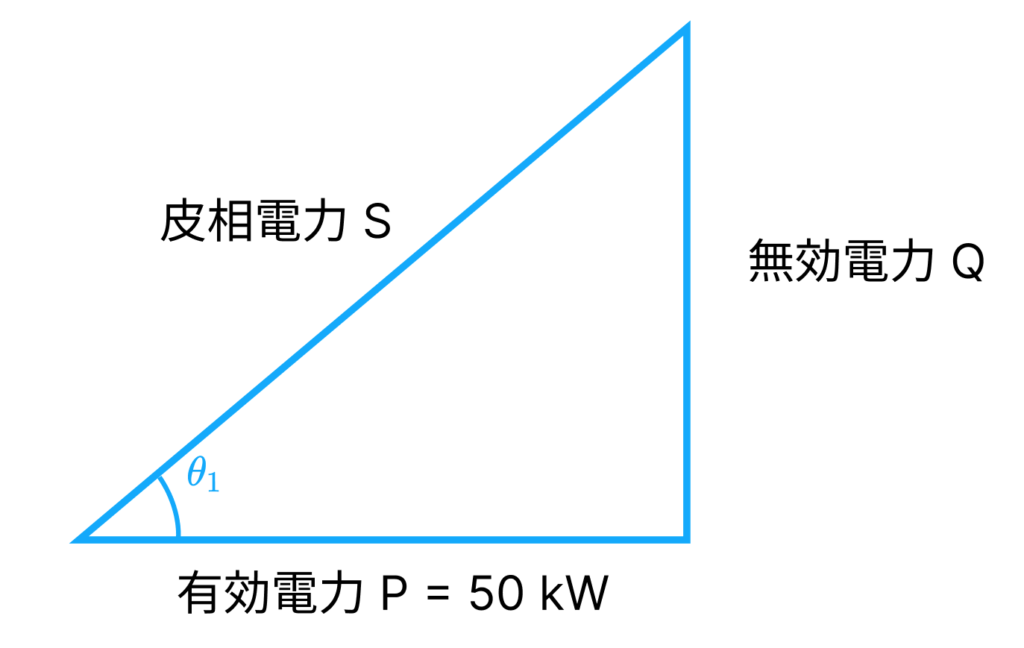
有効電力と \cos{\theta_1} = 0.7 が与えられているので、皮相電力 S, 無効電力 Qが求められます。
S = \frac{P}{\cos{\theta_1}} = \frac{50\mathrm{\,kW}}{0.7} \approx 71\mathrm{\,kW} Q = \sqrt{S^2 - P^2} = \sqrt{71^2 - 50^2} = 51\mathrm{\,kW}力率改善後のパワートライアングルは下図になります。
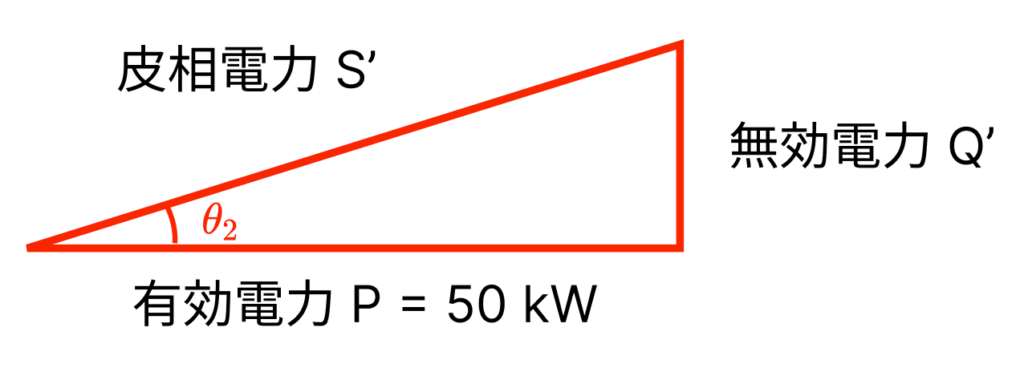
同様に、皮相電力 S’, 無効電力 Q’を求めてみます。
S' = \frac{P}{\cos{\theta_2}} = \frac{50\mathrm{\,kW}}{0.95} \approx 53\mathrm{\,kW} Q' = \sqrt{S'^2 - P^2} = \sqrt{53^2 - 50^2} = 16\mathrm{\,kW}したがってコンデンサは、
Q_C = Q - Q' = 51\mathrm{\,kW} - 16\mathrm{\,kW} = 35\mathrm{\,kW}の無効電力を供給すれば力率を0.95まで改善できます。
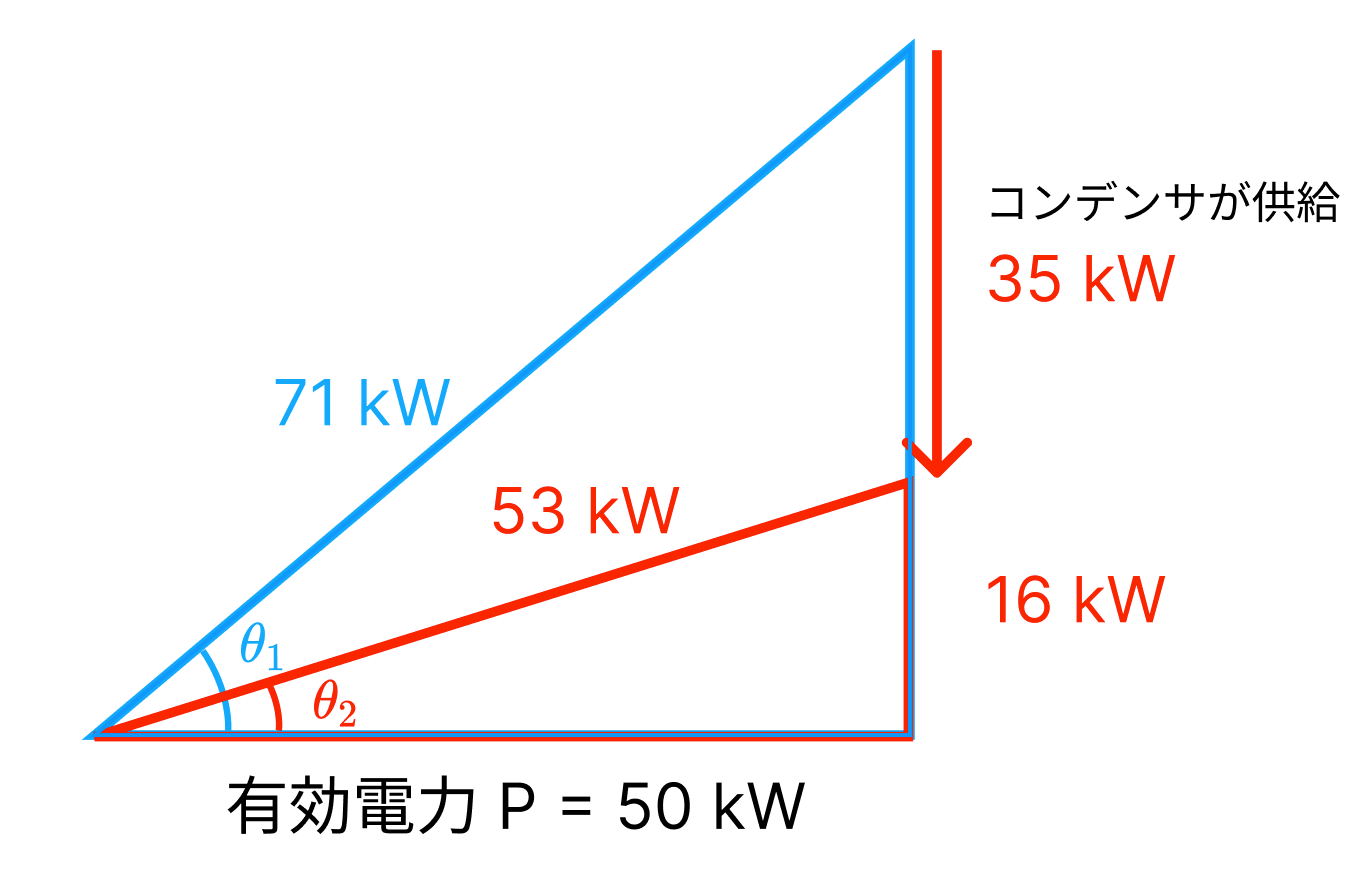
以上のことをまとめると下図になります。
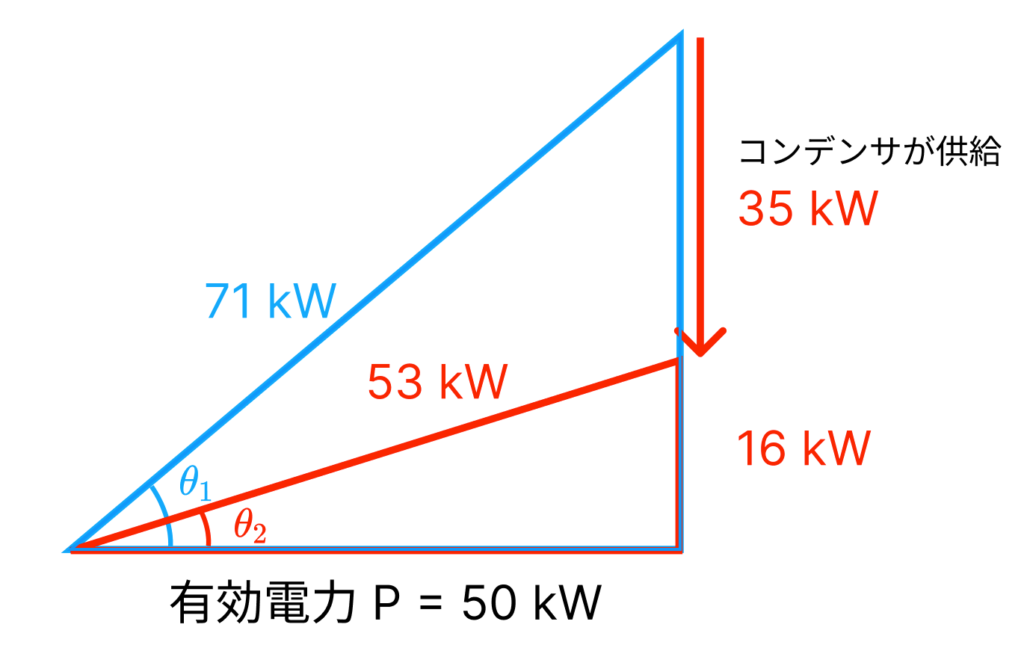
コンデンサが35 kWの無効電力を供給することで、無効電力が35 kW減少し、皮相電力も71 kWから53 kWまで削減できていることが分かります。
例題3: 電力料金に与える影響
ある工場が 100\mathrm{\,kW} の有効電力を使用している。力率が 0.7 の場合と 0.95 の場合で、必要な皮相電力(設備容量)を比較せよ。
必要な皮相電力は次のように求まります。
S_1 = \frac{100\mathrm{\,kW}}{0.7} \approx 143\mathrm{\,kW} S_2 = \frac{100\mathrm{\,kW}}{0.95} \approx 105\mathrm{\,kW}力率改善によって無効電力が減り、皮相電力が減少していることが分かります。
工場では、どちらも同じ有効電力を消費していますが、力率改善によって工場に供給する電力を減らすことができるため、送電線を流れる電流が小さくなり、設備の容量を小さくすることができます。
おわりに
この記事では、力率の例題を中心に、交流の電力や力率の定義について解説しました。
力率を理解する上で参考になれば幸いです。
ここまで読んでいただきありがとうございました。


コメント