はじめに
交流を数式で書くと、瞬時値やフェーザ、極形式など、様々な表示方法があって混乱しやすい分野です。特に、同じ表示方法でもいくつか呼び方があって分かりにくいと思います。
この記事では、交流の表示方法の違いを整理しながら、分かりやすく解説していきます。
それぞれの表示方法を使い分けることで、交流の計算が簡単になるので、ぜひ参考にしてください。
交流の4つの表示方法
交流の表示方法には、主に以下の4つの表示方法があります。

| 表示方法 | 式の例 | 特徴 |
|---|---|---|
| 瞬時値表示 | v(t) = 100\sqrt{2} \sin{(\omega t - 45\degree)} | 時間変化が分かりやすい 計算が面倒 |
| 複素数表示(直交形式) | \dot{V}=50\sqrt{2}+j50\sqrt{2} | 足し算・引き算が簡単 |
| 複素数表示(極形式) フェーザ表示 | \dot{V}=100 \angle{-45\degree} | 掛け算・割り算が簡単 |
| 指数関数表示 | \dot{V}=100 e^{j-45\degree} | 微分・積分が簡単 |
複素数表示には、直交形式、極形式、指数関数表示があり、極形式の方はフェーザ表示と呼ばれることが多いです。Vにドットがついているのは、複素数であることを区別するためです。
以下で、それぞれの表示方法について詳しく解説します。
瞬時値表示
瞬時値表示は次の式で表されます。
v(t) = \sqrt{2}V_{rms} \sin{(\omega t + \theta)} V_{rms} :電圧の実効値
\omega \ (= 2\pi f) :角周波数(fは周波数)
\theta :位相角(初期位相)
位相角(初期位相)は、基準となる電圧や電流に対する位相のずれを表します。
瞬時値表示では、時刻tが含まれているので、時間変化が直感的で波形がイメージしやすいですが、三角関数の計算が複雑になります。
そのため、計算では次の複素数表示を使うのが一般的です。
複素数表示では、時刻・周波数が省略されていて、振幅と位相のみを扱うため計算が簡単になります。
複素数表示
複素数表示には、直交形式、極形式(フェーザ表示)、指数関数表示の3つがあります。
直交形式
直交形式は次の式で表されます。
\dot{V} = x + jy虚部に i ではなく、 j が使われるのは、電流の i と混同しないためです。
ここで、xとyは、
x = V_{rms}\cos{\theta}, \ y=V_{rms}\sin{\theta} V_{rms} :電圧の実効値
\theta :位相角(初期位相)
で求めることができます。
直交形式の足し算・引き算は、実部と虚部を分けて計算するだけなので簡単です。
極形式(フェーザ表示)
極形式(フェーザ表示)は次の式で表されます。
\dot{V} = V_{rms}\angle{\theta} V_{rms} :電圧の実効値
\theta :位相角(初期位相)
フェーザ表示では、掛け算・割り算が簡単になります。
掛け算は、実効値同士を掛けて、位相角を足します。
\dot{V}_1 \dot{V}_2 = V_1 V_2 \, \angle{(\theta_1 + \theta_2)}割り算は、実効値を割って、位相角を引きます。
\frac{ \dot{V_1} }{ \dot{V_2} } = \frac{ V_1 }{ V_2 } \, \angle{(\theta_1 - \theta_2)}指数関数表示
指数関数表示は次の式で表されます。
\dot{V} = V_{rms} e^{j \theta} V_{rms} :電圧の実効値
\theta :位相角(初期位相)
指数関数では微分積分が簡単になります。
\theta = \omega t より、 v(t) = V_{rms} e^{j \omega t} とすると微分は、
\frac{d V(t)}{dt} = j \omega V_{rms} e^{j \omega t} = j \omega V(t)となり、 j\omega を掛けるだけです。
積分は、
\int V(t) dt = \frac{1}{j \omega} V_{rms} e^{j \omega t} = \frac{1}{j \omega} V(t)となり、 j\omega で割るだけなので簡単です。
例題
次の正弦波電圧を瞬時値形式、極形式、直交形式で表現せよ。
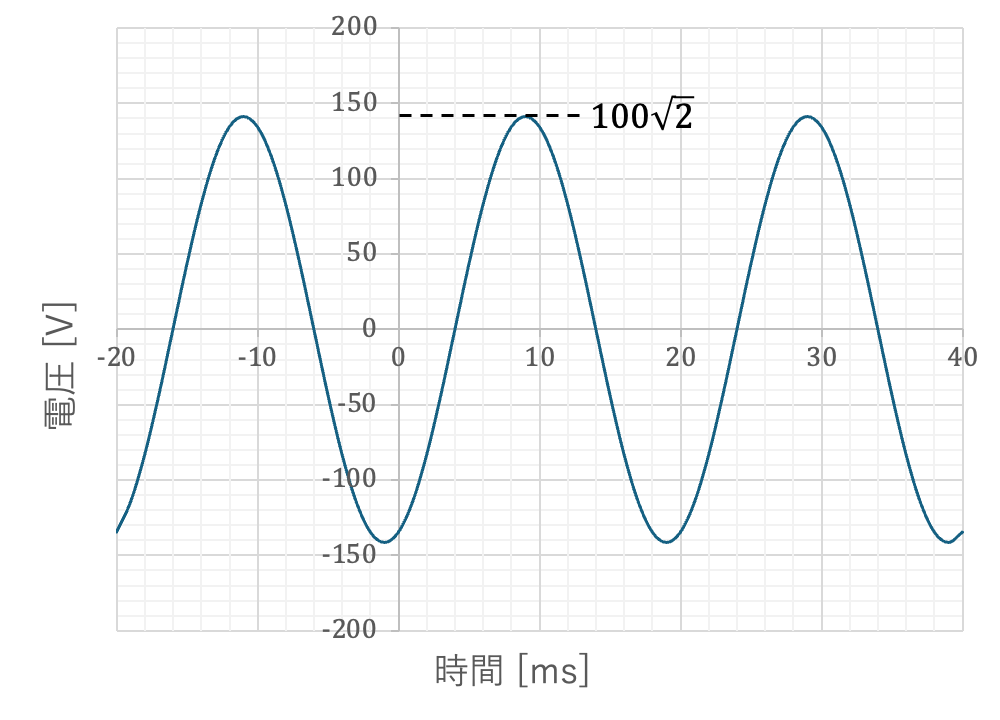
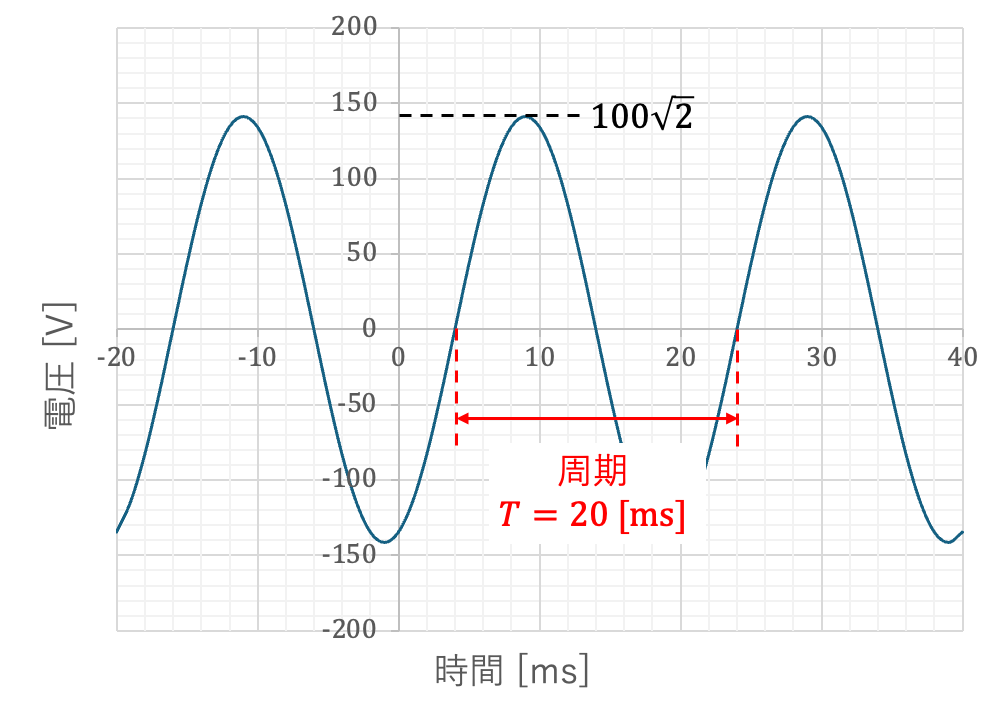
波形から、
周期 T = 20\mathrm{\,[ms]} = 20 \times 10^{-3} \mathrm{\,[s]} ,
振幅 V_{max} = 100\sqrt{2} \mathrm{\,[V]}
であることが読み取れるので、角周波数は、
\omega = 2\pi f, \,f = \frac{1}{T}を用いると、
\omega = 2\pi f = 2\pi \frac{1}{20 \times 10^{-3}} = 100\pi \mathrm{\,[rad/s]}と求まり、電圧の実効値は、
V_{rms} = \frac{V_{max}}{\sqrt{2}} = \frac{100\sqrt{2}}{\sqrt{2}} = 100\mathrm{\,[V]}と求まります。
次に、位相角(初期位相)を求めます。

上の図を見ると、今回の波形は、sin波が時間軸方法に右へ 4 [ms] 移動したものなので位相角は、
\theta = \omega t = 100\pi \times (-4 \times 10^{-3}) = -\frac{2}{5} \pi \mathrm{\,[rad]}と求まります。波形が右に移動している場合は、時刻tがマイナスになり、左に移動している場合は時刻tがプラスになります。また、位相角は通常 -\pi < \theta < \pi の範囲で表されます。
ここまでで角周波数、実効値、位相角が求まったので、瞬時値形式は、
v(t) = 100\sqrt{2} \sin{\left(100\pi t - \frac{2}{5} \pi \right)}極形式は、
\dot{V} = 100\angle{-\frac{2}{5} \pi}直交形式は、
\begin{aligned} \dot{V} &= V_{rms} \cos{\theta} + j V_{rms} \sin{\theta} \\ &= 100 \cos{\left( -\frac{2}{5} \pi \right)} + j 100 \sin{\left( -\frac{2}{5} \pi \right)} \\ &= 30.9 - j 95.1 \end{aligned}となります。
おわりに
この記事では、交流の4つの表現方法を図や例題を用いてまとめました。
交流回路の問題は、これらの表示方法を使い分けることで、非常に解きやすくなります。
ここまで読んでいただきありがとうございました。

コメント